fluSoft.de B H V D.de OrbitReader 20,20+, 40, Writer Meteor Vibrationsuhren Folienzeichengerät DrawFox Stockhalter DropMeNot B l i n d C a m.de YourDolphin.de Blindenhilfsmittel.biz Dolphin-Guide.de MiniGuide.de AngelEye.Vision SprachgesteuertesTelefon.de Ambutech.de BlindenBrief.de Dolphin-DE.de ZoomText.de Windows ZoomText-Mac.de MAC InfoDotBraille.com Deutscher Hilfsmittelvertrieb Vocally.de, Sprachsteuerung für Telefone Hilfsmittelvertrieb Dresdener Hilfsmittelvertrieb Deutscher Hilfsmittelversand WeisserStock.de SprachHandy.de RealSpeak Sprachsynthese Blindenschreibmaschine Tatrapoint Svarovsky-Stock.de alternative Formate NVDA, der freie ScreenReader TTS-Systeme.de Seika-Braille.com ZoomText.ch ZoomText.at OrCam 2.0 Deutscher Hilfsmittelvertrieb Suchstöcke für Feuerwehren FireCane.org Deutscher Hilfsmittelvertrieb OrCam MyEye OrCam MyReader PenFreiend3 Milestone ACE Orbit Braille TextAide Acapela TTS für NVDA OrCam Read



MS Rückenschwimmer MS Zukunft

---

fluSoft bei Google OrCam MyEye bei Google BHVD bei Google MiniGuide bei Google BlindenBrief bei Google

Falls man den Blindenstock beurteilen möchte, ist die Frage der Kriterienauswahl zu stellen. Neben den Gesichtspunkten wie Gefühle und Gewohnheiten einzelner Menschen, die subjektiven Charakter haben, gibt es auch Kriterien, die messbar und somit also objektiv sind.
Die erste Eigenschaft, die in Frage kommt, ist das Stockgewicht m. Um das sich aus der Stockhaltung in der horizontalen Ruhelage ergebende Gefühl (Bild 1) auszudrücken, ist das Gewicht nicht ausreichend. Es ist das sog. Kraftmoment M zu ermitteln, mit dem neben dem Gewicht die Schwerpunktlage berücksichtigt wird. Kraftmoment M ist durch das Produkt der durch das Stockgewicht m wirkenden und im Stockschwerpunkt konzentrierten Kraft F und dem Schwerpunktentfernung r vom Ergreifpunkt des Stockes (am besten vom oberen Stockende) gegeben:

M = F . r [Nm]

Die Kraft F ist durch Multiplizieren des Stockgewichts m in Kilogramm mit der Erdbeschleunigung g, deren Wert ungefähr 10 m/s²:

F = m . g [N]

Im Folgenden möchten wir ein anschauliches Beispiel anführen:
Gegeben sei ein Blindenstock mit Gewicht von 200 Gramm und Schwerpunkt in der Entfernung von 60 Zentimetern vom oberen Stockende. Für das Kraftmoment dieses Stocks gilt:

M = 0.2 . 10 . 0.6 = 1.2 Nm

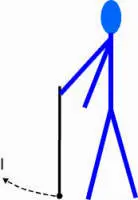Wer sich noch mehr mit der Beurteilung befassen möchte, kann darüber hinaus noch sog. Schwungmoment I ermitteln. Es ist eine dynamische Angabe, die eine Aussage darüber gibt, wie sich der Blindenstock beim Ausschwenken aus der vertikalen Gleichgewichtslage verhält (Bild 2). Es ist proportional der Anstrengung, die bei dieser Manipulation zu erbringen ist.
Die mathematische Berechnung des Schwungmoments ist verhältnismäßig kompliziert und erfordert, dass man das Stockgewicht über die Länge integriert. Diese Berechnungsart ist auszuweichen, indem man das Schwungmoment experimental mittels Schwungzeit t ermittelt, die Information über die Gewichtsverteilung beinhaltet. Das Schwungmoment des Blindenstockes ist dann durch einen Bruch gegeben, bei dem im Zähler das Produkt aus dem Stockgewicht m, der Erdebeschleunigung g, der Entfernung des Schwerpunktes vom oberen Ende r und der zweiten Potenz der Schwungzeit des Stockes t und im Nenner 4π² steht.

I = (m . g . r . t²) / 4π²

Das Produkt aus dem Stockgewicht m, dem Schwunggewicht g und der Schwerpuktentfernung r ist das bekannte Kraftmoment F, das einzusetzen ist:

I = (M . t²) / 4π²

Es ist noch die Schwungzeit zu ermitteln. Diese lässt sich zu ermitteln, in dem man den Stock aufhängt, das untere Ende in Bewegung bringt und die Zeit eines Schwungs misst (d.h. hin und her - Bild 3). Um bessere Genauigkeit zu erreichen, ist es günstiger, den Stock z.B. dreimal schwingen zu lassen und die ermittelte Zeit durch drei zu dividieren.
Im Folgenden möchten wir dazu ein Beispiel anführen. Nehmen wir den gleichen Stock mit der ermittelten gemessenen Schwungzeit von 2 Sekunden. Dann gilt für das Schwunggewicht dieses Stockes folgendes:

I = (0,2 . 10 . 0,6 . 22) / 4π² = (1,2 . 22) / 4π² = 0,12 kg.m²

Falls die oben angeführte Berechnung zu kompliziert erscheint, möchten wir die allgemeine Schlussfolgerung anführen:

Am besten ist ein Stock mit möglichst niedrigstem Gewicht, möglichst höchstgelegenem Schwerpunkt und möglichst kürzester Schwungzeit.